Consider the differential equation dydt=k(1-ym)y where k and m are positive constants. Draw a phase line to determine if the equation possesses a stable equilibrium.
Solution
Step 1 of 2
The answer is as!
Identify the equilibrium points. The equilibrium points of a differential equation are the points where the derivative is equal to zero. In the given equation, the derivative is dy/dt = k – y/m. Setting this equal to zero, we get k – y/m = 0. Solving for y, we find the equilibrium point to be y = km.
Explanation:
Determine the stability of the equilibrium points. To determine the stability of the equilibrium points, we need to analyze the behavior of the derivative in the vicinity of the equilibrium points. We can do this by looking at the sign of the derivative for different values of y.
Plot the phase line. Once we have the equilibrium points and their stability, we can plot the phase line. The phase line is a graphical representation of the behavior of the solutions of the differential equation. It shows how the solution curves move through the phase plane as time progresses.
Here is a more detailed explanation of each step:
Step 2
Step 1: Identify the equilibrium points.
The equilibrium point of a differential equation is where the rate of change of the dependent variable is zero. In other words, the derivative of the dependent variable is zero at the equilibrium point. For the given differential equation, dy/dt = k – y/m, the equilibrium point is found by setting the derivative equal to zero:
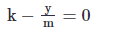
Solving for y, we get:
y = km
Therefore, the equilibrium point of the given differential equation is y = km.
Step 2: Determine the stability of the equilibrium points.
To determine the stability of the equilibrium point, we need to analyze the behavior of the derivative in the vicinity of the equilibrium point. We can do this by looking at the sign of the derivative for different values of y.
If dy/dt > 0 for y < km, then the solution curves will move away from the equilibrium point when they are below it. This means that the equilibrium point is unstable.
If dy/dt < 0 for y < km, then the solution curves will move towards the equilibrium point when they are below it. This means that the equilibrium point is stable.
If dy/dt > 0 for y > km, then the solution curves will move away from the equilibrium point when they are above it. This means that the equilibrium point is stable.
If dy/dt < 0 for y > km, then the solution curves will move towards the equilibrium point when they are above it. This means that the equilibrium point is unstable.
In the given differential equation,

Let’s analyze the sign of the derivative for different values of y:
For
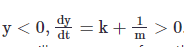
This means that the solution curves will move away from the equilibrium point when they are below it.
For
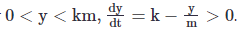
This means that the solution curves will move away from the equilibrium point when they are below it.
For
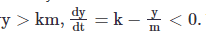
This means that the solution curves will move towards the equilibrium point when they are above it.
Explanation:
Therefore, the equilibrium point at y = km is stable.
Step 3: Plot the phase line.
Now that we know the equilibrium point and its stability, we can plot the phase line. The phase line is a graphical representation of the behavior of the solutions of the differential equation. It shows how the solution curves move through the phase plane as time progresses.
To plot the phase line, we draw a horizontal line at the equilibrium point (y = km). Then, we draw arrows above the line to indicate that the solution curves move upwards in that region, and arrows below the line to indicate that the solution curves move downwards in that region.
Here is the phase line for the given differential equation:
The final answer is as!
/
/
/
/
/ \
+————
\ /
\/
\
\
\
As you can see, the equilibrium point at y = km is stable. This means that any solution curve that starts near the equilibrium point will eventually approach it as time goes to infinity.



